Des chercheurs de la Swanson School of Engineering de l’Université de Pittsburgh ont développé, par simulation informatique, un système de matériaux mous capable de convertir directement des signaux chimiques en mouvement mécanique. Cette étude, centrée sur les réseaux chimico-mécaniques dans les matériaux synthétiques, explore de nouvelles voies pour obtenir un mouvement autonome sans recourir à des équipements électroniques complexes.

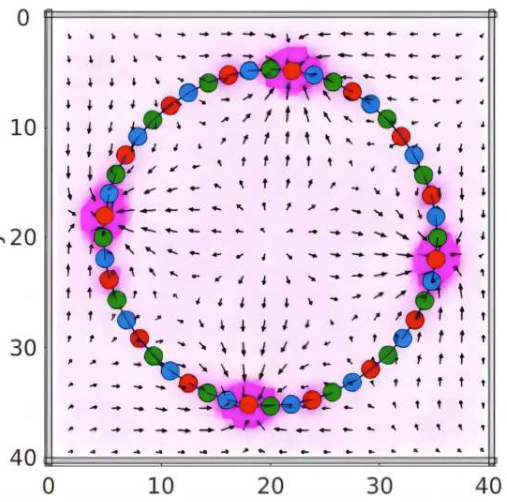
Le chercheur assistant Oleg E. Shklyaev, en collaboration avec la professeure Anna C. Balazs du département de génie chimique et pétrolier, a publié ces résultats dans la revue PNAS Nexus. Leur système de matériaux mous imite les mécanismes de mouvement des organismes biologiques les plus simples, en convertissant des ondes chimiques en mouvement mécanique via un réseau chimico-mécanique composé de microbilles recouvertes d’enzymes. Balazs déclare : « Quel est le système le plus simple capable de reproduire ce comportement dans des matériaux synthétiques ? »

Le cœur du système repose sur un réseau de microbilles recouvertes d’enzymes reliées par des connecteurs flexibles. Lorsque des réactions chimiques se produisent à la surface des billes, les variations de concentration générées provoquent des mouvements de fluide, entraînant une déformation du réseau. Shklyaev décrit : « Cela ressemble à un mille-pattes ou à un ver plat, où une onde de contraction traverse le corps pour le propulser vers l’avant. » Les chercheurs ont réussi à contrôler les caractéristiques de propagation des ondes en ajustant la géométrie du réseau chimico-mécanique.

La particularité de ce réseau chimico-mécanique réside dans sa capacité de mouvement auto-entretenu. Balazs explique : « Ce système peut « indiquer » à des zones spécifiques de se mettre en mouvement. Il s’agit d’un système nerveux autonome réduit à sa forme la plus simple — un mécanisme guidé chimiquement. » Par rapport aux matériaux à réponse stimulée traditionnels, ce système basé sur des réseaux chimico-mécaniques peut générer une gamme plus large de comportements dynamiques.